type
status
date
slug
summary
tags
category
icon
password
Property
C.L.Hwang 和 K.Yoon 于1981年首次提出 TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution)。TOPSIS 法是一种常用的组内综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。基本过程为基于归一化后的原始数据矩阵,采用余弦法找出有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制,数据计算简单易行。
通俗的例子:小明数学考试 134 分,要怎么知道他的成绩是好还是不好呢?
基于分布的评价方法会观察小明的分数位于班级分数的哪个水平(如前 5%、前 10%),但这种评价方法只能给出一个方向的情况。如班上成绩除了最高分外,其余都是 134 分,那么小明的成绩就是并列的倒数第一,但是正向评价给出的结果是前 5%。 而 TOPSIS 就是找出班上最高分(假设是 147 分)、最低分(假设是 69 分),然后计算小明的分数和这两个分数之间的差距,从而得到自己分数好坏的一个客观评价。距离最高分越近,那么评价情况越好,距离最低分越近,那么评价情况越糟。
TOPSIS过程

指标属性同向化,一般选择指标正向化
TOPSIS 法使用距离尺度来度量样本差距,使用距离尺度就需要对指标属性进行同向化处理(若一个维度的数据越大越好,另一个维度的数据越小越好,会造成尺度混乱)。通常采用成本型指标向效益型指标转化(即数值越大评价越高,事实上几乎所有的评价方法都需要进行转化),此外,如果需要使用雷达图进行展示,建议此处将所有数据都变成正数。
极小型指标:期望指标值越小越好(如患病率、死亡率等)

M为指标 x可能取值的最大值
中间型指标:期望指标值既不要太大也不要太小,适当取中间值最好(如水质量评估 PH 值)
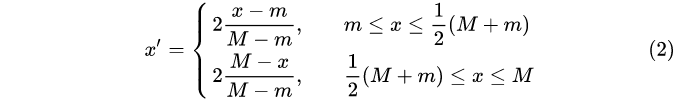
其中M为指标 x的可能取值的最大值, m为指标 x 的可能取值的最小值
区间型指标:期望指标的取值最好落在某一个确定的区间最好(如体温)
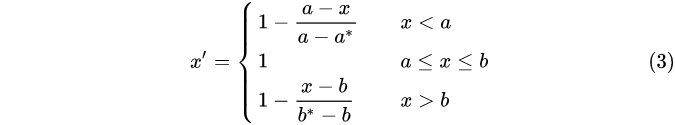
其中 [a,b] 为指标 x的最佳稳定区间, [a*,b*] 为最大容忍区间
构造归一化初始矩阵
设共有n个待评价对象,每个对象都有m个指标(属性),则原始数据矩阵构造为:
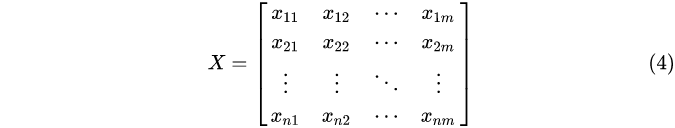
构造加权规范矩阵,属性进行向量规范化,即每一列元素都除以当前列向量的范数(使用余弦距离度量)
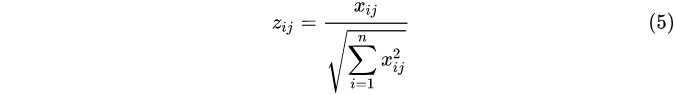
由此得到归一化处理后的标准化矩阵 Z :

确定最优方案和最劣方案
最优方案Z+由Z中每列元素的最大值构成:
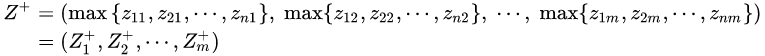
最劣方案 Z- 由Z中每列元素的最小值构成:
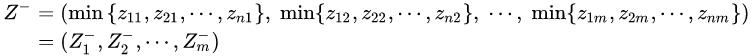
计算各评价对象与最优方案、最劣方案的接近程度
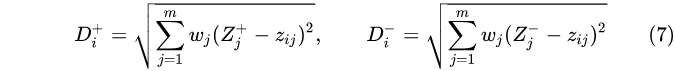
其中wj为第 j 个属性的权重(重要程度),指标权重建议根据实际确定或使用专家评估方法。
计算各评价对象与最优方案的贴近程度Cj
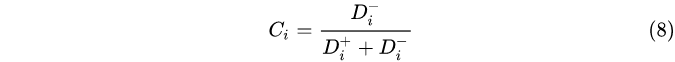

根据Ci大小进行排序,给出评价结果
案例
