type
status
date
slug
summary
tags
category
icon
password
Property
红黑树,是一种平衡二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是 Red 或 Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出2倍,因而是接近平衡的。
AVL树和红黑树:
- AVL树:严格平衡(左右子树高度差不超过1),所以AVL树的查找、插入、删除效率高: ,但插入和删除节点后,要维持树的平衡状态,做的旋转处理还是很多的
- 红黑树:近似平衡(控制最长路径不超过最短路径的2倍),变了一种方式来控制树的平衡,相较于AVL树,没有那么严格
红黑树更多是一种折中的选择,它舍弃平衡二叉树的严格平衡,换取节点插入时尽可能少的调整。
红黑树的特点:
- 树的每一个节点都有一个颜色
- 根节点是黑色
- 不能出现连续的红色节点(如果一个节点是红色的,则它的两个孩子结点必须是黑色的)
- 从根节点到每一个叶子节点的路径上,黑色节点的数量是相同的
- 空节点是黑色

为什么满足以上性质后,就能保证 最长路径中节点个数不会超过最短路径中节点个数的2倍?

当某条路径最短时,这条路径必然都是由黑色节点构成。当某条路径长度最长时,这条路径必然是由红色和黑色节点交替构成的。而从任一节点到其每个叶子节点的所有路径必须包含相同数量的黑色节点,这么来说最长路径上的黑节点的数目和最短路径上的黑节点的数目相等。
最短路径:全是黑节点,最长路径:一黑一红,交替出现,所以最长路径刚好是最短路径的2倍。
红黑树和AVL树效率对比
对于一棵拥有 n 个内部结点(不包括NIL叶子结点)的红黑树,树的最大高度为
当红黑树是一颗满二叉树时,高度最小 ,当红黑树中最长路径刚好是最短路径2倍的时候,红黑树的高度最大
操作 | AVL | 红黑树 |
是否为平衡树 | 是 | 否 |
增删查时间复杂度 | ||
插入时的最多旋转次数 | 2 | 2 |
删除时的最多旋转次数 | 3 |
如果数据量是10亿:
查找效率 | 查找次数(约等于) |
AVL树: | 30 |
红黑树: | 60 |
- 虽然AVL树的查找效率优于红黑树,但对于现在的CPU,查找30次和60次是没有什么区别的,可以认为红黑树和AVL树的查找效率几乎是一样的,简化后为
- 红黑树整体性能略优于AVL树(因为红黑树旋转情况少于AVL树)
- 红黑树的插入删除比AVL树更便于控制操作
- 红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是 ,红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
红黑树的插入
红黑树的插入过程与 BST 树的插入过程基本类型,不同的地方在于,红黑树插入新的节点后,需要进行调整,以满足红黑树的性质。根据红黑树第五条性质,即从根节点到空叶节点的所有路径上的黑色节点的数目相同,为了减少操作的复杂度,对于新插入的节点,需要将其设置为红色。
当红黑树为空树时,插入节点后,将根节点更改为黑色,以满足红黑树的第三条性质,即根节点是黑色。
当红黑树非空时,插入的节点为红色,此时要检查其父节点的颜色:
- 如果父节点是黑色,那么插入完成。
- 如果父节点是红色,那么为了保持红黑树的性质,则需要做出相对应的调整。
- 如果是下图所示的情况,即新节点的叔叔节点为红色节点,如果将祖父节点和父亲节点交换颜色,那么则会导致祖父节点和叔叔节点均为红色,不满足红黑树的第四条性质。因此,此时需要将父亲节点和叔叔节点均变为黑色,将祖父节点变为红色,然后递归向上调整整个红黑树。
- 如果是下图所示的情况,即新节点的叔叔节点为黑色节点,且新节点、父亲节点和祖父节点在同一侧。此时不能仅仅交换父亲节点和祖父节点的颜色,虽然这样做满足了没有连续的红色节点的性质,但是调整前左侧路径有 1 个黑色节点,右侧路径有 2 个黑色节点,调整后左、右路径都只有 1 个黑色节点,对于右侧路径而言,其调整后比调整前少了 1 个黑色节点,此时必然不会满足红黑树的第五个性质,即从根节点到每一个叶子节点的路径上,黑色节点的数量是相同的。因此,此时需要在此基础上再进行一次右旋操作:
- 如果是下图所示的情况,即新节点的叔叔节点为黑色,但是新节点和父亲节点、祖父节点并不在同一侧。如果按照上一个情况的处理方式进行操作,即先交换父亲节点和祖父节点的颜色,然后由于叔叔节点所在的路径的黑色节点数目比操作前少了一个,因此进行一次右旋操作,可以看到,右旋后,有两个红色节点相连,不满足红黑树的性质。因此,当前这种情况并不能做出这样的调整,正确的处理方式是对当前节点和其父亲节点做一次左旋操作,将当前节点、父亲节点和祖父节点调整到同一侧,此时就会转变为上一种情况:



红黑树的删除
对于红黑树的删除操作而言,它是在 BST 树删除操作的基础上进行删除的,由于 BST 树的删除分为三种情况,即有两个子节点、有一个子节点、没有子节点,其中有两个子节点可以通过删除前驱节点/后继节点转化为第二种情况,那么总的来说,都是要将被删除节点的孩子节点放到其父节点的地址域中。因此,红黑树的删除操作可以分为如下几种情况:
- 如果删除的是一个红色节点,那么其子节点和父节点一定为黑色,此时就是一颗 BST 树的删除,无需做任何调整;
- 如果删除的是一个黑色节点,那么一定有某条路径上的黑色节点数目变少了,此时不满足红黑树第五条性质,所以需要做出相应的调整,分为如下两种情况:
- 如果补上来的孩子节点是红色,那么直接将这个孩子涂成黑色,调整完成;
- 如果补上来的孩子节点是黑色,此时需要从其兄弟节点处借一个黑色节点以弥补缺失的黑色节点的数目,此时又会分为四种情况;
- 如果是下图所示的情况,即删除的节点在左边,其右边的兄弟是黑色的,且兄弟的右孩子是红色的。那么首先应该交换兄弟节点和其父节点的颜色,然后对父节点进行左旋操作,最后再将兄弟节点的右孩子变为黑色即可:
- 如果是下图所示的情况,即删除的节点在左边,其右边的兄弟是黑色,且兄弟的左孩子是红色。由于需要在兄弟节点上借一个黑色节点,且借完之后需要在兄弟节点处找到一个红色节点进行变色,弥补缺失的黑色节点。因此如果按照情况 1 的处理方式,对待删除节点的父节点进行一次左旋转操作,那么兄弟节点的红色节点就会跑到左子树上来,此时,兄弟节点便无法利用红色节点来弥补缺失的黑色节点,因此,此种处理方式不可取。
- 如果是下图所示的情况,即删除的节点在左边,其右边的兄弟是黑色,且兄弟的两个孩子也都是黑色。此时,无法向兄弟借黑色节点,因为借之后兄弟无法弥补缺失的黑色节点。因此需要将所有路径上的黑色数目都减少一个,那么先将兄弟节点涂为红色,然后让 node 指向删除结点的父节点,如果父节点为红色,那么将其变为黑色即可;如果父节点为黑色,那么此时就需要查看父节点的兄弟节点,继续落在这几种情况的范围内,不断向上回溯调整:
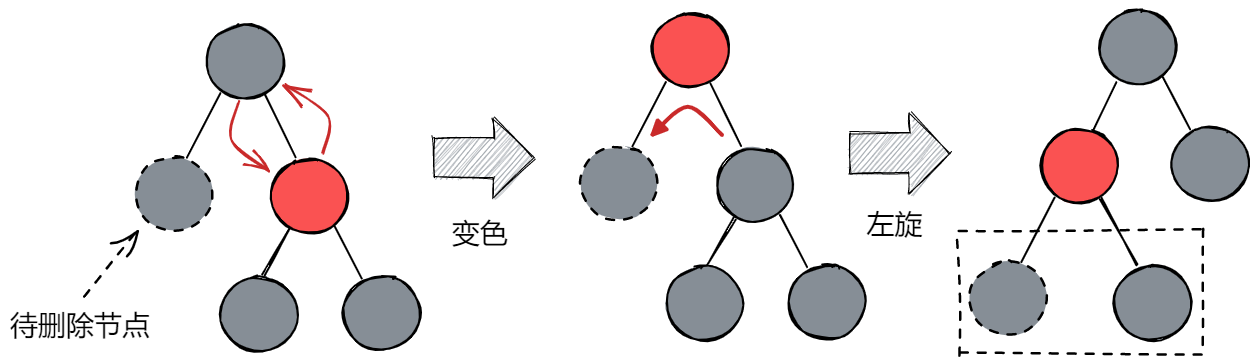
- 如果是下图所示的情况,即删除节点在左边,其右边的兄弟为红色,那么根据红黑树的性质,兄弟节点的父亲及其两个孩子节点均为黑色。此时,应该先交换兄弟节点和父亲节点的颜色,然后对父亲节点执行左旋操作,操作完成后,此时待删除结点的兄弟节点就会变为黑色,那么就会又转变为上面三种情况:

正确的处理方式应该是先对兄弟节点进行一次右旋操作,然后交换兄弟节点和红色节点的颜色,此时就会转变为情况1: