双指针与滑动窗口
2023-3-4
| 2023-8-2
0  |  阅读时长 0 分钟
type
status
date
slug
summary
tags
category
icon
password
Property
 
目录
目录
对撞指针两数之和 II - 输入有序数组三数之和最接近的三数之和有效三角形的个数盛最多水的容器验证回文串验证回文串 II回文链表调整数组顺序使奇数位于偶数前面下一个排列下一个更大元素 III接雨水快慢指针环形链表环形链表II删除有序数组中的重复项压缩字符串移动零长度最小的子数组分离双指针两个数组的交集 II相交链表滑动窗口滑动窗口最大值最小覆盖子串最大连续1的个数 III
 
双指针（Two Pointers）：指的是在遍历元素的过程中，不是使用单个指针进行访问，而是使用两个指针进行访问，从而达到相应的目的。如果两个指针方向相反，则称为对撞指针。如果两个指针方向相同，则称为快慢指针。如果两个指针分别属于不同的数组 / 链表，则称为分离双指针。
 

对撞指针

对撞指针：指的是两个指针left、right分别指向序列第一个元素和最后一个元素，然后left指针不断递增，right不断递减，直到两个指针的值相撞（即left == right），或者满足其他要求的特殊条件为止。
 

两数之和 II - 输入有序数组

题目：给你一个下标从1开始的整数数组 numbers ，该数组已按非递减顺序排列 ，从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。以长度为2的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。可以假设每个输入只对应唯一的答案 ，而且不可以重复使用相同的元素。
示例：
 
 

三数之和

题目：给一个整数数组nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]]满足i != j、i != k且j != k ，同时还满足nums[i] + nums[j] + nums[k] == 0 。返回所有和为0且不重复的三元组。
示例：
 
 

最接近的三数之和

题目：给一个长度为n的整数数组nums和 一个目标值target。请从nums中选出三个整数，使它们的和与target最接近。返回这三个数的和。假定每组输入只存在恰好一个解
示例：
 
 
 

有效三角形的个数

题目：给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数
示例：
notion image
  • 由于可能是乱序的，故需要先排序，满足要求的3个数的下标记作 (一直满足 )
  • 先固定个下标中的一个(推荐固定 )，使用对撞指针
  • 统计时当确定时，使用贪心思想可以得到该趟的组合数量
  • 最后对每一趟得到的数量求和
 
 
 
 

盛最多水的容器

题目：给定一个长度为n的整数数组height 。有n条垂线，第i条线的两个端点是(i, 0)和(i, height[i]) 。找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
示例：
notion image
设两指针，指向的水槽板高度分别为 ，此状态下水槽面积为 。由于可容纳水的高度由两板中的短板决定，因此可得面积公式 :
notion image
在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度−1变短：
  • 若向内移动短板 ，水槽的短板 可能变大，因此下个水槽的面积可能增大 。
  • 若向内移动长板 ，水槽的短板 不变或变小，因此下个水槽的面积一定变小
因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积
算法流程：
  1. 初始化： 双指针分列水槽左右两端
  1. 循环收窄： 直至双指针相遇时跳出
    1. 更新面积最大值
    2. 选定两板高度中的短板，向中间收窄一格
  1. 返回值： 返回面积最大值
 
 

验证回文串

题目：如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个回文串。字母和数字都属于字母数字字符。给一个字符串 s，如果它是回文串 ，返回true ；否则，返回false 。
示例：
 

验证回文串 II

题目：给一个字符串 s，最多可以从中删除一个字符。判断s是否能成为回文字符串：如果能，返回true ；否则，返回false 。
示例：
 

回文链表

题目：给一个单链表的头节点head ，请你判断该链表是否为回文链表。如果是，返回true ；否则，返回false 。
示例：
notion image
将值复制到数组中后用双指针法
 
 

调整数组顺序使奇数位于偶数前面

题目：输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数在数组的前半部分，所有偶数在数组的后半部分
示例：
 

下一个排列

题目：
整数数组的一个 排列  就是将其所有成员以序列或线性顺序排列。
  • 例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。
  • 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
  • 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
  • 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ，找出 nums 的下一个排列。必须 原地 修改，只允许使用额外常数空间。
示例：
 
从倒数第二个数开始向前遍历，找到一个最小的大于当前数的值，使之交换值之后，对后方数值进行重拍列，则比为下一个排列，若最后都没找到则将nums进行重排列
 

下一个更大元素 III

题目：给你一个正整数 n ，请你找出符合条件的最小整数，其由重新排列 n 中存在的每位数字组成，并且其值大于 n 。如果不存在这样的正整数，则返回 -1 。注意 ，返回的整数应当是一个 32 位整数 ，如果存在满足题意的答案，但不是 32 位整数 ，同样返回 -1 。
示例：
把 n转换成字符串（字符数组），那么本题实际上是在求字符数组的 下一个排列，当不存在下一个排列时返回-1。
 
 
 
 
 

接雨水

题目：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例：
notion image
雨水面积为图中的蓝色部分，想要计算蓝色部分我们可以先考虑计算出蓝色+黑色的面积作为总面积，再使用总面积 - 黑色部分面积也就是陆地面积。
计算总（陆地 + 雨水）面积：一层一层求出每一层的面积后求和
 
首先定义一个前一层高度preHeight，初始化为0
步骤1、左指针右移、右指针左移并跳过所有高度小于等于前一层高度的点
步骤2、当前层高度（左右指针较小的值 - 前一层高度preHeight）* 该层宽度，并加入总面积中，同时更新前一层高度preHeight
重复1、2步骤
 
计算第一层（1 - 0）*（11 - 1 + 1） = 11，更新preHeight = 1
notion image
计算第二层（2 - 1）*（10 - 3 + 1） = 8，更新preHeight = 2
notion image
计算第三层（3 - 2）*（7 - 7 + 1） = 1 ，更新preHeight = 3
 
 
 

快慢指针

快慢指针：指的是两个指针从同一侧开始遍历序列，且移动的步长一个快一个慢。移动快的指针被称为快指针（fast），移动慢的指针被称为慢指针（slow）。两个指针以不同速度、不同策略移动，直到快指针移动到数组尾端，或者两指针相交，或者满足其他特殊条件时为止。

环形链表

题目：给一个链表的头节点 head ，判断链表中是否有环。如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。如果链表中存在环 ，则返回 true 。 否则，返回 false 。
示例：
notion image
定义两个指针，一快一慢。慢指针每次只移动一步，而快指针每次移动两步。初始时，慢指针在位置head，而快指针在位置head.next。这样一来，如果在移动的过程中，快指针反过来追上慢指针，就说明该链表为环形链表。否则快指针将到达链表尾部，该链表不为环形链表。
 

环形链表II

题目：
给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改 链表。
示例：
notion image
notion image
设链表中环外部分的长度为。 指针进入环后，又走了的距离与相遇。此时，指针已经走完了环的圈，因此它走过的总距离为。
根据题意，任意时刻， 指针走过的距离都为指针的2倍。因此，有
从相遇点到入环点的距离加上 圈的环长，恰好等于从链表头部到入环点的距离。
因此，当发现与相遇时，再额外使用一个指针。起始，它指向链表头部；随后，它和每次向后移动一个位置。最终，它们会在入环点相遇。
 
 
 
 
 
 

删除有序数组中的重复项

题目：给一个升序排列的数组nums，原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致
示例：
 
notion image
 
数组是有序的，那么重复的元素一定会相邻。要求删除重复元素，实际上就是将不重复的元素移到数组的左侧。
用2个指针，一个在前记作 p，一个在后记作 q，比较 p和q位置的元素是否相等。如果相等，q后移 1 位；如果不相等，将 q  位置的元素复制到 p+1 位置上，p后移一位，q后移 1 位。重复过程，直到 q等于数组长度。返回 p + 1 ，即为新数组长度。
 
 

压缩字符串

题目：给你一个字符数组 chars ，请使用下述算法压缩：
从一个空字符串s开始，对于chars中的每组连续重复字符 ：
  • 如果这一组长度为1 ，则将字符追加到s中。
  • 否则，需要向s追加字符，后跟这一组的长度。
压缩后得到的字符串 s 不应该直接返回 ，需要转储到字符数组 chars 中。需要注意的是，如果组长度为 10 或 10 以上，则在 chars 数组中会被拆分为多个字符。
请 修改完输入数组后 ，返回该数组的新长度。必须设计并实现一个只使用常量额外空间的算法来解决此问题。
示例：
 
每次当读指针移动到某一段连续相同子串的最右侧，就在写指针处依次写入该子串对应的字符和子串长度即可。
当读指针位于字符串的末尾，或读指针指向的字符不同于下一个字符时，就认为读指针位于某一段连续相同子串的最右侧。该子串对应的字符即为读指针指向的字符串。使用变量记录该子串的最左侧的位置，这样子串长度即为。
 
 
 
 
 
 

移动零

题目：给定一个数组nums，编写一个函数将所有0移动到数组的末尾，同时保持非零元素的相对顺序。
示例：
 
定义一个慢指针slow，初始化为0，表示非零元素的位置。 定义一个快指针fast，初始化为0，表示遍历数组的位置。 使用一个循环，从头到尾遍历数组nums。 在循环中，如果快指针指向的元素不等于0，就将它赋值给慢指针指向的位置，然后将慢指针向后移动一位。 在循环结束后，将慢指针后面的所有元素都置为0。
 
 
 

长度最小的子数组

题目：给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0
示例：
 
 
 

分离双指针

分离双指针：两个指针分别属于不同的数组 / 链表，两个指针分别在两个数组 / 链表中移动。
 

两个数组的交集 II

题目：两个整数数组 nums1和 nums2，以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。
示例：
如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。首先对两个数组进行排序，然后使用两个指针遍历两个数组。初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，将该数字添加到答案，并将两个指针都右移一位。当至少有一个指针超出数组范围时，遍历结束。
 
 

相交链表

题目：
给两个单链表的头节点 headA 和 headB ，请找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
图示两个链表在节点 c1 开始相交：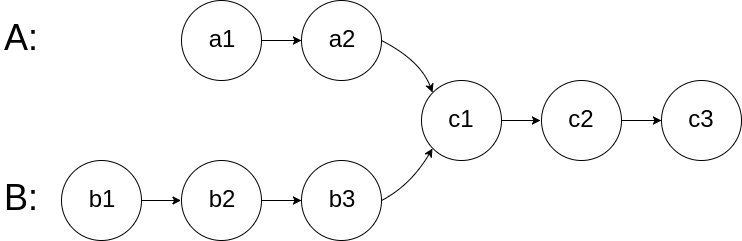
notion image
题目数据 保证 整个链式结构中不存在环。注意，函数返回结果后，链表必须保持其原始结构 。
 
自定义评测：
评测系统 的输入如下（你设计的程序不适用 此输入）：
  • intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
  • listA - 第一个链表
  • listB - 第二个链表
  • skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
  • skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被视作正确答案 。
 
示例：
notion image
 
交点不是数值相等，而是指针相等
 
 
 

滑动窗口

在计算机网络中，滑动窗口协议（Sliding Window Protocol）是传输层进行流控的一种措施，接收方通过通告发送方自己的窗口大小，从而控制发送方的发送速度，从而达到防止发送方发送速度过快而导致自己被淹没的目的。我们所要讲解的滑动窗口算法也是利用了同样的特性。
滑动窗口算法（Sliding Window）：在给定数组 / 字符串上维护一个固定长度或不定长度的窗口。可以对窗口进行滑动操作、缩放操作，以及维护最优解操作。
  • 滑动操作：窗口可按照一定方向进行移动。最常见的是向右侧移动。
  • 缩放操作：对于不定长度的窗口，可以从左侧缩小窗口长度，也可以从右侧增大窗口长度。
滑动窗口利用了双指针中的快慢指针技巧，可以将滑动窗口看做是快慢指针两个指针中间的区间，也可以将滑动窗口看做是快慢指针的一种特殊形式。
 
滑动窗口算法一般用来解决一些查找满足一定条件的连续区间的性质（长度等）的问题。该算法可以将一部分问题中的嵌套循环转变为一个单循环，因此它可以减少时间复杂度。按照窗口长度的固定情况，可以将滑动窗口题目分为以下两种：
  • 固定长度窗口：窗口大小是固定的
      • 求解步骤：假设窗口的固定大小为 window_size
      1. 使用两个指针 left、right。初始时，left 、right 都指向序列的第一个元素，即：left = 0，right = 0 ，区间 [left, right] 被称为一个「窗口」。
      1. 当窗口未达到 window_size 大小时，不断移动 right，先将 window_size 个元素填入窗口中。
      1. 当窗口达到 window_size 大小时，判断窗口内的连续元素是否满足题目限定的条件。
        1. 如果满足，再根据要求更新最优解。
        2. 然后向右移动 left，从而缩小窗口长度，即 left += 1，使得窗口大小始终保持为 window_size。
      1. 向右移动 right，将元素填入窗口中。
      1. 重复 2 ~ 4 步，直到 right 到达序列末尾。
  • 不定长度窗口：窗口大小是不固定的
      • 求解步骤：
      1. 使用两个指针 left、right。初始时，left、right 都指向序列的第一个元素。即：left = 0，right = 0，区间 [left, right] 被称为一个「窗口」。
      1. 将区间最右侧元素添加入窗口中，即 window.add(s[right])。
      1. 然后向右移动 right，从而增大窗口长度，即 right += 1。直到窗口中的连续元素满足要求。
      1. 此时，停止增加窗口大小。转向不断将左侧元素移出窗口，即 window.popleft(s[left])。
      1. 然后向右移动 left，从而缩小窗口长度，即 left += 1。直到窗口中的连续元素不再满足要求。
      1. 重复 2 ~ 5 步，直到 right 到达序列末尾。
 
 

滑动窗口最大值

题目：
给一个整数数组nums，有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。
示例：
 
 
其实滑动窗口类似于数据结构双端队列，窗口向右滑动过程相当于向队尾添加新的元素，同时再把队首元素删除。
notion image
队列中没必要维护窗口中的所有元素，可以在队列中只保留那些可能成为窗口中的最大元素，去掉那些不可能成为窗口中的最大元素。
考虑这样一种情况，如果新进来的数字大于滑动窗口的末尾元素，那么末尾元素就不可能再成为窗口中最大的元素了，因为这个大的数字是后进来的，一定会比之前先进入窗口的小的数字要晚离开窗口，因此就可以将滑动窗口中比其小的数字弹出队列，于是队列中的元素就会维持从队头到队尾单调递减，这就是单调递减队列。
notion image
对于队列内的元素来说：
  • 在队列内自己左边的数就是数组中左边第一个比自己大的元素。
  • 当被弹出时，遇到的就是数组中右边第一个比自己大的元素 ，只要元素还在队列中，就意味着暂时还没有数组中找到自己右侧比自己大的元素
  • 队头到队尾单调递减，队首元素为队列最大值
 
 
 
 

最小覆盖子串

题目：给一个字符串s 、一个字符串 t 。返回s中涵盖t所有字符的最小子串。如果s中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。
示例：
notion image
一个用于「延伸」现有窗口的 指针，和一个用于「收缩」窗口的 指针。在任意时刻，只有一个指针运动，而另一个保持静止。在上滑动窗口，通过移动指针不断扩张窗口。当窗口包含全部所需的字符后，如果能收缩，就收缩窗口直到得到最小窗口。
判断当前的窗口包含所有 所需的字符呢？可以用一个哈希表表示中所有的字符以及它们的个数，用一个哈希表动态维护窗口中所有的字符以及它们的个数，如果这个动态表中包含的哈希表中的所有字符，并且对应的个数都不小于的哈希表中各个字符的个数，那么当前的窗口是「可行」的。
 
 
 
 
 

最大连续1的个数 III

题目：给定一个二进制数组 nums 和一个整数 k，如果可以翻转最多k个0 ，则返回数组中连续1的最大个数 。
示例：
统计窗口内0的个数 ，则问题转换成在 的前提下，窗口大小的最大值。
 
相关文章 :
计算机基础
  • 计算机基础
  • 数据结构与算法
    • graph 题目排序
    目录